Goodnite Bob Productions is a company that designs and manufactures small-batch puzzles of unusual designs. You can find these puzzles, as well as many other math teaching materials at the SamizdatMath online store.

Houdini’s Curse: A Vintage Puzzle

This puzzle was found in Houdini’s Paper Magic, a book written by the magician and escape artist Harry Houdini. In the book, Houdini devotes a section to paper puzzles in which geometric shapes are dissected and re-arranged to create new shapes. Some of the designs are highly popular, including the well-known Chinese tangram. Houdini named the above puzzle “The Symmetrical Square Puzzle,” and after quite a bit of research, I was unable to locate a version that was manufactured using durable materials. For the first time in over 90 years, this puzzle has been manufactured in a small batch on 1/8″ acrylic and precision cut using a laser cutter. You can purchase “Houdini’s Curse” at my online Etsy store.

Van Hiele Tiles: An Excellent Puzzle for Teaching Geometry

A second puzzle that I manufacture is based on the “Lott Stone Puzzle” or the “Sphinx Puzzle,” which is copied from a design by the Anchor Stone Company, which manufactured this pattern during the 18th and 19th century. This pattern is no longer manufactured; antique “stone” versions have been spotted on Ebay. However, you may purchase them individually or in classroom sets of 30, laser cut from 1/8″ acrylic, at my online teachers’ store, SamizadatMath.

This puzzle was described in an article by the mathematical researcher, Pier van Hiele, who explained how it could be used to engage children in geometric thinking. You can download the template for cutting out this puzzle, as well as 16 different puzzles to solve by clicking here.

Why do I love this puzzle so much? It has many unusual properties that are not found in other geometric puzzles. Let’s begin with the triangles:

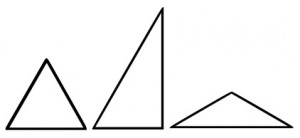
If you notice, there are three distinct types of triangles here, which cover every single attribute possible. If you classify the triangles by angles, we have an acute, a right and an obtuse triangle in our collection. Classify them by the relationship of the sides to one another, we have an equilateral (all sides equal), scalene (no sides equal) and isosceles (2 sides equal.)

Our set of shapes also includes three different quadrilaterals:

We start out with a very standard looking rectangle, followed by a “textbook” trapezoid (that is, isosceles) and then a third “non-standard” trapezoid that has a set of adjacent sides that are equal, which doesn’t make it isosceles by the way, because, unlike triangles, it does matter which two sides are equal.

Adding to the interest is this: every shape can be used to make congruent or similar replications of every other shape. That is, you can take two shapes, and make another version of the same shape.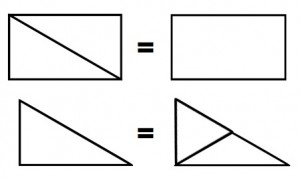 

Of course, you can’t make the two smallest shapes, the isosceles obtuse triangle, and the equilateral triangle, by combining the other, larger shapes, but you can make “dilated” versions of the two by combining two shapes:

This can be repeated, so that all 7 shapes can be combined to make larger versions of all the “basic” shapes in the set.

My long term project has been to “re-create” the original puzzle that was published in 1911. Because the original pieces and puzzle booklet are very hard to find (even on Ebay), I’ve decided to release my own version as a tribute to the original. The original booklet had over 100 different shapes that could be made using a single set of puzzles; right now I’m offering a “gift box” version of the puzzle made from 1/8″ laser cut acrylic with 24 individual designs printed on heavy card stock.